[ad_1]
What is the biggest natural selection achievable? By using the phrase normal, I have ruled out the risk that you simply just solution infinity (∞) to torpedo the guessing game. But even if we authorized infinitely massive values, this reaction would induce troubles. What about ∞ + 1, ∞2 or ∞∞? If persons set ahead these replies to the premier natural amount question, who would be proper?
The respond to is no one particular because infinity is not an standard number that follows the normal guidelines of calculation. For illustration, the amount line is infinite, no matter of whether you start off it at –∞, or 1. As a result, a statement this sort of as ∞ + 1 will make no feeling. On top of that, there are dissimilarities even with infinite values: infinity does not constantly equivalent infinity. Consequently, infinity would not be a assured winner in a greatest number contest.
It took humankind quite a few millennia to comprehend this strategy and forged it into a neat theory. At the end of the 19th century, mathematician Georg Cantor laid a basis for the mathematical notion of infinity by thinking about quantities and their dimension. For illustration, 1, 2, 3, 4 and x, y, z, q each consist of 4 factors each and thus have a size of 4, which authorities connect with a “cardinality of 4.”
The organic quantities , 1, 2, 3,…, on the other hand, have infinitely a lot of components. We can insert 1 to any purely natural quantity the result is also a organic range. If we now seem at the set of all even figures , 2, 4,…, we could possibly presume that it is just 50 percent as large—after all, only each and every second normal amount is contained in it. But Cantor acknowledged that both of those sets (the pure and the even figures) have the exact cardinality.
Matching Sets and Countable Infinities
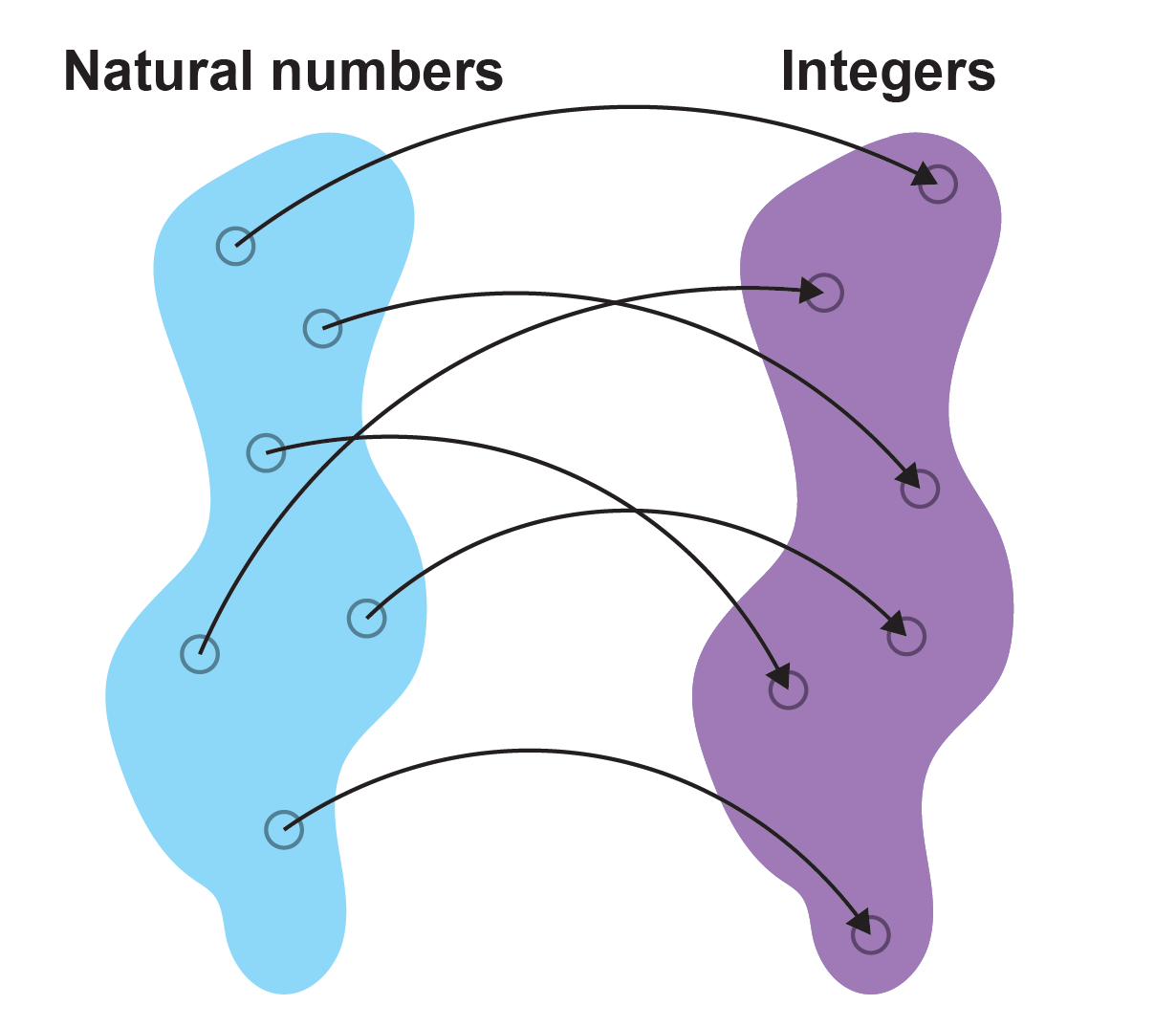
As talked about in a further column of mine, Cantor arrived to this surprising final result when he when compared the components of two sets. If you want to discover out no matter if a set A (for illustration, men and women at a bus prevent) is just as huge as an additional set B (absolutely free seats on a bus), you can assign an ingredient from B to each element from A. If there are even now folks left standing at the end, then A is more substantial than B. If, on the other hand, there are nevertheless cost-free seats, then B ought to be greater than A.
But if you can assign just one seat to every single man or woman, then both sets are exactly the exact same dimensions and hence have the similar cardinality. In this way, Cantor also studied the cardinality of infinite sets. For case in point, you can map any purely natural number to particularly a single even range, say, by forming the pairs (,), (1,2), (2,4), (3,6),…, (n, 2n). The mapping performs out specifically. Neither purely natural nor even numbers continue being at the close. Therefore, both of those sets comprise the same variety of things.

In this article an crucial lesson emerges. When it comes to infinities, do not go with your intestine. These ideas are almost never intuitive.
Not only is the cardinality of organic and even numbers the very same, the trick with mapping two sets can be utilized to other examples as nicely. For case in point, the set of all odd numbers is the very same sizing as the set of all natural ones—as is the set of all integers (which incorporate adverse values), primary quantities and even the rational numbers (which involve fractions). For each and every of these sets, there is a mapping that uniquely assigns a pure amount 1, 2, 3,… to every single factor. That suggests you could—at minimum theoretically—number the factors of these sets (if you had infinite time and leisure).
The smallest infinity owes its title to this reality. The cardinality of the purely natural figures is identified as “countably infinite” and is represented by ℵ (spoken as “aleph zero”). So as an alternative of publishing the reply “infinity” to the largest quantities opposition, you could offer ℵ.
The sets introduced so much all have the very same cardinality. But actual figures break the sample. If, in addition to the rational numbers, you also enable irrational values, these kinds of as the sq. root of 2, pi or Chaitin’s consistent, then the set abruptly gets so massive that you can no more time enumerate its elements—even if the record is infinitely lengthy.
The Infinity of Actual Quantities Exceeds All-natural Quantities
Cantor proved this actuality with his second “diagonal argument.” This is a evidence by contradiction: you start with the assumption that there are countably infinite actual numbers and derive a contradictory statement from this concept (that is, “There can’t be countably infinite actual numbers”).
To continue, you do not have to consider all true figures. It is adequate to believe that all real values among and 1 are countable (which, we will quickly see, is improper).
Appropriately, you could generate all these values in an infinitely lengthy listing, with one below the other. For example:
.32476834567854765 …

.84737834527845745 …

.78347864586745768 …

.78347863763547879 …

…
How the list is sorted does not make any difference. The only crucial detail is that it is total. If we can genuinely depend all of the values, our checklist must contain every single actual range amongst and 1. But Cantor shown that he could build an additional quantity involving and 1 that does not show up in the checklist.
He did it in the adhering to way: the 1st decimal position of the new amount corresponds to the very first decimal put of the to start with quantity in the list as well as one—that is, 4 in the higher than example. The second decimal area is acquired by calculating the second decimal put of the second range moreover one—that is, 5. For the 3rd, you enhance the 3rd decimal spot of the 3rd selection by 1, and so on. (If you strike a 9 you can transform the value to a .)

In this way, an irrational amount with an infinite selection of decimal locations will be acquired. It does not surface in the record due to the fact it always differs in at minimum just one digit from every single range listed. Hence, the list simply cannot be total, which contradicts the original assumption. Cantor could thus conclude that there are “uncountably many” true figures.
A Provably Unprovable Assumption
Moreover the cardinality ℵ of the pure quantities, there is at the very least a single additional (uncountable) infinity—and it may be a superior decision than ℵ in the level of competition to obtain the largest number.
Just how massive is the set of genuine numbers? Cantor requested himself this exact same problem when he was investigating irrespective of whether a established of figures existed that would be much larger than the normal figures but lesser than the real figures. Discovering no these set, the mathematician formulated his famous “continuum hypothesis” in 1878. It states that there is no established whose cardinality lies amongst that of the normal numbers and that of the true numbers.
But Cantor could not show his assumption—nor could any person else. As it turns out, the continuum hypothesis belongs to the statements that elude our fundamental mathematical framework. They are provably unprovable: you can neither prove nor disprove the conjecture by the regular mathematical signifies. (Kurt Gödel proved that there is these kinds of incompleteness in each individual significant formulation of mathematics in 1931.)
In other terms, you could assume the continuum speculation to be genuine and never ever encounter a contradiction. Conversely, nevertheless, you could postulate that there are other infinities between the cardinality of the organic and true numbers—and face no problems possibly. This is not especially enjoyable for mathematicians. Immediately after all, we are talking about the sizing of the authentic numbers—nobody understands how many of these values exist. In response, some individuals are striving to extend the basic framework of the topic to derive a instrument from this bigger idea to confirm or disprove the continuum hypothesis.
Authorities are by no usually means united in this work. The basis of mathematics, the “Zermelo-Fraenkel set principle,” is composed of 9 unproved basic statements (so-identified as axioms) that sort a basis for the total subject. It took various attempts to obtain a ideal set of axioms for the activity due to the fact it need to satisfy numerous requirements. The established should really have as number of axioms as achievable, and they should be intuitively real and not much too intricate. Other examples are the axiom of the empty set, which states that a set without the need of aspects exists, and the axiom of pairing, according to which two sets with the very same elements are equivalent.
The 9 axioms of the Zermelo-Fraenkel set principle (alongside one another with the axiom of alternative) are ample to build up the mathematics that we know. But the continuum hypothesis eludes them. In purchase to look into the cardinality of the true figures in a lot more element, you have to extend the recent established concept to consist of other fundamental statements. For case in point, you could append the statement “The continuum hypothesis is true” to the group of axioms. This would not be a superior axiom, even so. Contrary to the other statements, it is not straight obvious why this a person should really be correct.
Therefore, specialists are wanting for other axioms that are intuitively genuine and can be utilized to investigate the continuum speculation. There are previously a couple of promising candidates—some would confirm Cantor’s conjecture, even though other folks would refute it. Which extended edition of set theory will prevail, if any, remains to be witnessed. As very long as this is the situation, the issue of how many serious numbers exist remains unsolved.
Even if that continues to be a secret, it has lengthy been recognised that there are sets with significantly bigger cardinalities than that of the set of serious numbers—even although the true figures are by themselves infinite. And if you want to gain the largest range video game, you ought to go chase the biggest infinity.
This short article at first appeared in Spektrum der Wissenschaft and was reproduced with authorization.
[ad_2]
Resource backlink


