[ad_1]
Have faith in but validate. That expression captures the rigidity concerning relying on many others though nevertheless wanting to keep some amount of management around a scenario. Mathematician Adi Shamir must have believed about this challenge when he formulated what is now acknowledged as “Shamir’s secret sharing,” an algorithm named immediately after him.
To realize it, the subsequent puzzle can support: Suppose an elderly girl wishes to bequeath the contents of her risk-free, which is secured with a mixture lock, to her five sons, but she is suspicious of every of them. She fears that if she reveals the code to just 1, he will make off with the contents. So she would like to give each individual son a clue this kind of that only the 5 functioning jointly can open the safe and sound. How really should the woman carry on?
The undertaking could seem to be easy. For case in point, if the mix lock needed a 5-digit code, she could give every single son a quantity so that they could open it jointly. But in that situation, if a few sons teamed up, they could likely bypass their two other brothers. Three allies are only two figures brief of the overall code, so they could swiftly test out the achievable number combos to get to the coveted contents.
The lady is for that reason looking for a way to distribute information that can only be made use of if all five perform collectively. If two, three or four of the five sons get together, the combined data articles will have to be useless. And that need tends to make the task substantially much more elaborate.
But in 1979 this obstacle did not discourage Shamir. Two a long time before he experienced produced the so-referred to as “RSA algorithm” alongside one another with Ron Rivest and Leonard Adleman. It was the first uneven encryption algorithm to be greatly adopted, and it is however used right now.
Shamir’s Key Sharing in Motion
To understand the Shamir magic formula-sharing strategy, it assists to look at a concrete numerical example. Suppose the woman’s solution code is 43953, and, for the sake of simplicity, let us suppose she only has two sons. (We’ll do the job our way up to the problem with five sons later on.)
If the female were to entrust just one son with “439” and the other with “953,” she would have specified the two of them the exact sum of details. Now, as explained above, the sons could each and every test to guess the missing two digits. They would only have to consider a greatest of 100 combos each and every to open the safe and sound.
Shamir consequently necessary a distinct solution. It would be greatest if every sons obtained a piece of info that at initially look experienced absolutely nothing to do with the resolution. But if you put the two items of information together, you ought to be equipped to deduce the selection mix 43953. And there is an classy, simple way to do this with the assist of a linear equation.
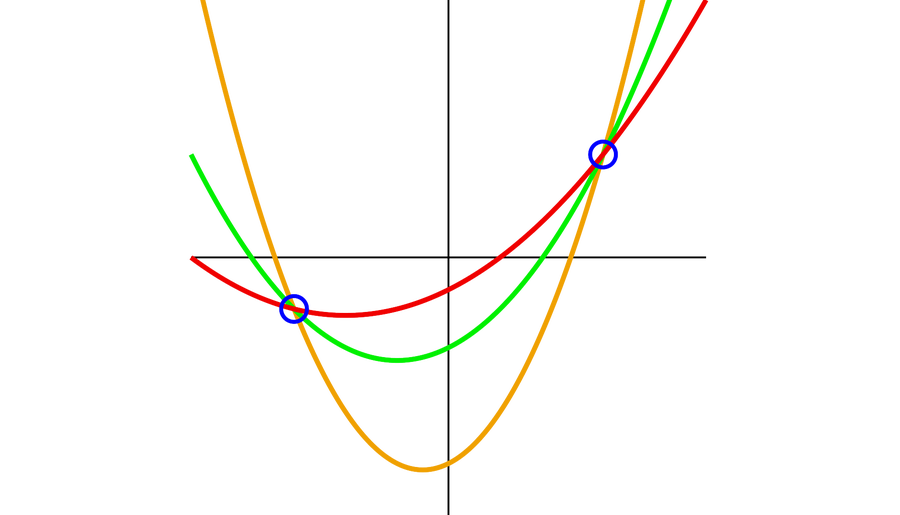
Each and every straight line is uniquely described by two details. Shamir understood that the magic formula quantity can be encoded in a straight line: for case in point, as the top at which it intersects the y axis. If you give the two sons the coordinates of one particular position each individual on the straight line, they can only identify the variety 43953 together. One particular of the sons are not able to do anything at all with a solitary issue by itself: there are an infinite range of straight strains that run by a single place.
The lady could, for case in point, select the equation of the line y = 5x + 43953 and give the eldest son the coordinates for a stage P1 (33503, 211468) and the other son the coordinates for a next place, P2 (85395, 470928). Even if the two sons are bad at math, they can merely mark the two points in the aircraft, hook up them with a ruler and then read off the issue at which the straight line intersects the y axis for the remedy to the safe and sound.
So the difficulty is solved for two sons. If the girl has three sons, she could continue in a equivalent way. In this case, nonetheless, she would not choose a straight line but fairly a parabola to cover the code.
For instance, the female can pick out the quadratic perform y = 5x2 + 10x + 43953 and give each individual of her sons a point on the parabola. Yet again, the stage of intersection with the y axis corresponds to the desired answer: 43953. Two of the sons cannot conspire in opposition to the 3rd simply because an infinite quantity of parabolas can run as a result of two factors the two sons have to have the enable of their brother to come across the place of intersection with the y axis and consequently the code to the protected.
The basic principle can be generalized for any selection of get-togethers: A woman with 4 sons can resolve an equation of the form y = ax3 + bx2 + cx + 43953. (Since 3 is the greatest exponent in this equation, it is termed a polynomial equation of the 3rd degree.) A female with 5 sons makes use of a polynomial equation of the fourth degree (these as y = ax4 + bx3 + cx2 + dx + 43953), and so on. The theory is based mostly on so-referred to as polynomial interpolation: in standard, n + 1 factors are demanded to uniquely figure out a polynomial of the nth degree.
The woman can also give her sons obtain to the risk-free in pairs. In this case she relies on the sons managing every other this sort of that two out of five people require to be current to open up the safe. To do this, the girl can all over again pick out a straight line as a base and mark five randomly chosen factors on it. By offering just about every son a issue, she guarantees that two of them can identify the code—regardless of which two of the sons fulfill.
But there’s a catch. Let us return to the state of affairs with the 5 sons. If 4 of them conspire in opposition to a brother, they can use the four factors to clear up the fourth-diploma equation as significantly as achievable. Of training course, they can not examine the code instantly from it. In the conclusion they are remaining with an equation with two unknowns: a parameter a and the code c (which in our example is 43953, but the sons do not know that).
The 4 sons know that c ought to be an integer, even so. And if, for illustration, the girl has always given them integer coordinates for the details on the curve, then they can believe that a in all probability also has an integer price. This significantly restricts the selection of choices. The brothers can use a computer plan to attempt out diverse solutions—and could then determine the appropriate code.
Into a Various Quantity Array
To stay away from this kind of a situation, Shamir had another trick up his sleeve: instead of calculating with the typical genuine figures, he restricted himself to a smaller sized amount space: a finite industry. In this range procedure, the four primary arithmetic operations (addition, multiplication, subtraction and division) can be applied as common. Alternatively of an infinite amount of figures, on the other hand, this amount place only is made up of a finite number of them.
While that may perhaps sound unfamiliar, we use finite fields just about every day—for instance, anytime we glimpse at the clock. If you only search at the hours, the quantity assortment contains either 12 or 24 quantities. But we however calculate in this limited space: if it is 11 P.M. and someone states that the bakery opens in 7 several hours, then it’s very clear that they signify six o’clock.
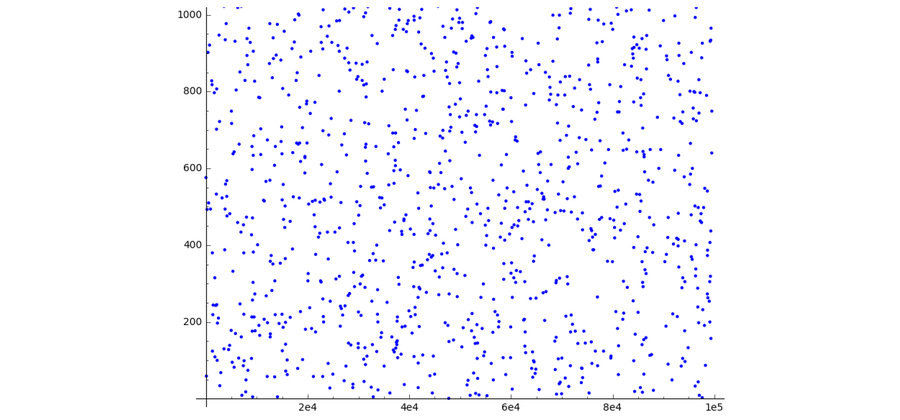
In Shamir’s mystery sharing, a restricted quantity selection is also chosen, but the upper restrict is normally a large primary amount. If the number room is chosen in this way, the graph of a polynomial no more time corresponds to a steady curve but to randomly distributed details in the airplane.
By limiting the woman’s calculations to these types of a variety variety, it is nearly extremely hard for the brothers to conspire against each other. To find out the appropriate numerical code, they have to get the job done with each other.
This article initially appeared in Spektrum der Wissenschaft and was reproduced with permission.
[ad_2]
Supply website link