[ad_1]
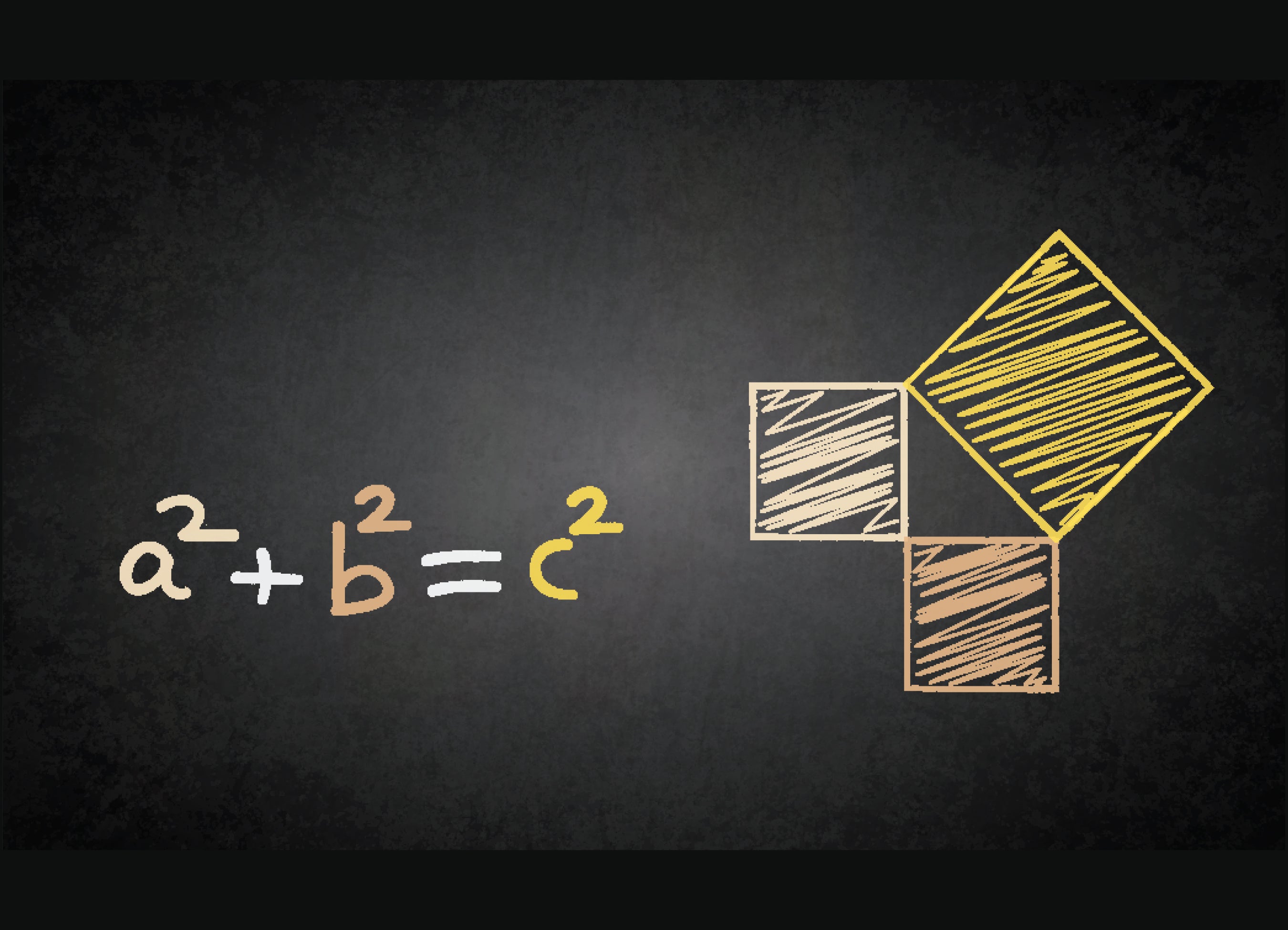
Two superior school students have proved the Pythagorean theorem in a way that one particular early 20th-century mathematician believed was impossible: using trigonometry.
Calcea Johnson and Ne’Kiya Jackson, the two at St. Mary’s Academy in New Orleans, declared their achievement last month at an American Mathematical Culture meeting. “It’s an unparalleled emotion, actually, because there’s just almost nothing like it, becoming able to do one thing that … men and women really don’t think that youthful men and women can do,” Johnson informed WWL-Television, a New Orleans CBS affiliate.
If confirmed, Johnson and Jackson’s evidence would contradict mathematician and educator Elisha Loomis, who stated in his 1927 e-book The Pythagorean Proposition that no trigonometric evidence of the Pythagorean theorem could be appropriate. Their perform joins a handful of other trigonometric proofs that had been included to the mathematical archives above the a long time. Every single sidestepped “circular logic” to verify the pivotal theorem. So what accurately is a trigonometric proof of the Pythagorean theorem, and why was Loomis so closed off to the notion?
The Pythagorean theorem offers an equation to calculate the longer side of a correct triangle by summing the squares of the other two sides. It is normally phrased as a2 + b2 = c2. In this equation, a, b and c characterize the lengths of the a few sides of a suitable triangle, a triangle with a 90-diploma angle concerning two of its sides. The amount c is the duration of the longest aspect, termed the hypotenuse. Although the theorem is named for the historical Greek philosopher Pythagoras, some historians believe it was acknowledged in Babylon all-around 1,000 decades previously.
The theorem “connects algebra and geometry,” states Stuart Anderson, a professor emeritus of arithmetic at Texas A&M University–Commerce. “The assertion a2 + b2 = c2, that’s an algebraic statement. But the determine that it comes from is a geometric a single.”
In the meantime trigonometry focuses on capabilities that rely on angles. These functions, this kind of as the sine and cosine, are outlined applying proper triangles. Envision a ideal triangle with one particular aspect that lies flat from a desk and one more that shoots straight up from exactly where it fulfills the initial side at a right angle. The hypotenuse will achieve diagonally involving these two sides.
Now measure the angle in between the hypotenuse and the desk. Mathematicians define the sine of this angle as the height of the vertical side divided by the duration of the hypotenuse. The cosine of this angle is the duration of the horizontal aspect divided by the hypotenuse. The Pythagorean theorem is thus equivalent to the equation sin2 x + cos2 x = 1. “A great deal of the essential trig ‘identities’ are very little more than Pythagoras’ theorem,” clarifies Anderson, referring to equations that explain associations amid different trigonometric features.
Loomis believed that if you utilised these functions in a proof of the Pythagorean theorem, you would have assumed the theorem to begin with—a circular argument and consequently an unforgivable mathematical error.
But which is not normally genuine. In their talk at the American Mathematical Modern society conference, Jackson and Johnson claimed a trigonometric identification referred to as the law of sines didn’t depend on the Pythagorean theorem and that they could use it to establish the theorem.
Anderson hopes that Jackson and Johnson’s evidence will increase fascination in mathematics amid college students. “It sort of would make me wish I continue to experienced a course so I could communicate about it,” he suggests.
The other trigonometric proofs of the theorem that have appeared in the past contain a couple of that are described on mathematician Alexander Bogomolny’s web site. One of these was crafted by Jason Zimba, then a physicist and mathematician at Bennington Faculty, and printed in Discussion board Geometricorum in 2009. This proof made use of a trigonometric id that permits you to work out the cosine and sine of an angle x – y devoid of making use of the Pythagorean theorem—if you know the cosines and sines of x and y on their very own.
On Oct 26, 2009, Bogomolny included Zimba’s proof to his web page, writing “Elisha Loomis, myself and no question numerous other individuals considered and continue to feel that no trigonometric evidence of the Pythagorean theorem is attainable…. I happily confess to currently being in the erroneous.” In excess of time, Bogomolny included additional trigonometric proofs to the web-site: 1 these kinds of proof could be written in just 4 lines.
The saga exhibits how even the most basic arithmetic can shock us. “Mathematicians, I think, have discovered to not make a daring assert that something is unachievable because we’ve been embarrassed about the several years way too quite a few times by accomplishing that,” Anderson suggests.
The American Mathematical Society has inspired the New Orleans pupils to submit their proof for publication in a peer-reviewed scientific journal.
[ad_2]
Source link


