[ad_1]
In 1852 a South African mathematician questioned a seemingly simple query that induced unlimited dispute, still left a path of overturned publications in its wake and culminated in a resolution that has stretched the incredibly tenets of math.
The coloration conundrum that stirred up so much difficulties: What is the fewest number of hues necessary to coloration a map so that no neighboring states or other specified parts have the same hue? Here’s how it is effective. Verify out the map of the contiguous U.S. below.


It appears a minor bare-bones. To make maps extra vivid and plainly emphasize their borders, cartographers are inclined to colour in the locations like so:
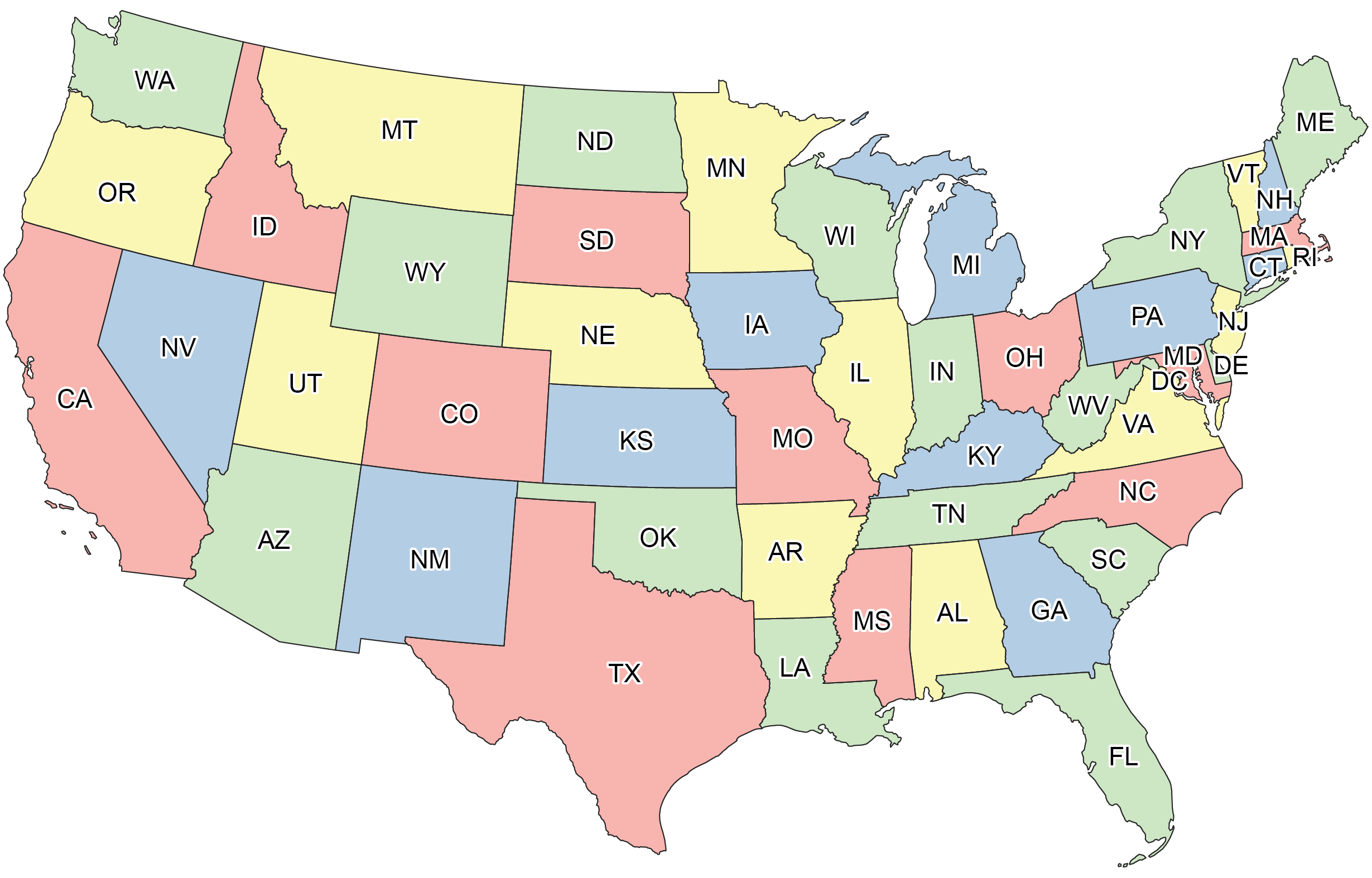


The natural way, we really don’t want neighboring states to have the very same coloration, because that would make the boundaries more complicated. Under this constraint, we utilized 4 colours to fill in the map earlier mentioned. Could we have completed it with only three? Could possibly other maps demand 5 or 6?
The map does not need to correspond to authentic geography—any partitioning of a flat surface area into unique locations qualifies. The question is, offered any these kinds of map, what is the minimum range of hues essential to fill in each location so that no two adjacent regions have the very same colour? Some floor policies: just about every region must be contiguous, so technically Michigan violates the set up since Lake Michigan severs the condition into two disconnected parts. For two regions to rely as adjacent, they ought to share some contiguous border touching at a one position (or discrete established of factors) does not qualify. For instance, Utah and New Mexico famously only touch at a corner and so do not depend as neighbors for our needs.
With the policies proven, here are some queries with surprising responses. Suppose I printed out a large poster with a challenging map containing a couple thousand locations. How extensive would it acquire you to figure out no matter whether the map could be colored with two colours? 3 hues? 4 hues? You never automatically want to uncover a coloring, just determine whether or not a coloring exists for just about every range of colors. Curiously, although these 3 tasks appear nearly similar, they each and every need radically distinct amounts of time to entire. Making use of the finest-recognized procedures:
- 
- Determining regardless of whether two colors suffice would get about an hour. To do it, select out any location and decide on a shade for it, say, crimson. This forces all of the region’s neighbors into the other coloration, say, blue. In switch, all of their neighbors come to be crimson, and so on, propagating by the map. At some point you possibly face a conflict in which neighboring locations share a coloration, in which situation no “two-coloring” exists, or the colors unfold by the complete map conflict-free of charge, in which case you have found a legitimate coloring. A again-of-the-envelope calculation with 3,000 regions at a rate of 1 2nd for each coloring yields 50 minutes of time very well spent.
- Suppose the map can not be stuffed with only two colours. Deciding whether or not a few shades suffice would consider for a longer period. The afternoon would pass you by. The months would peel off the calendar as you furiously scribbled unlimited configurations, looking for just one that operates. To have forth, you’d have to go down the ongoing activity to your little ones and they to their youngsters. Generations of life devoted to absolutely nothing other than finding a a few-coloring of this map wouldn’t place a dent in the workload as the sun inevitably engulfs the Earth in some billions of years and places an close to the foolish endeavor, leaving us scarcely closer to an answer. Deciding no matter whether an arbitrary map has a three-coloring is tough. Listed here “hard” is a technical expression indicating that it falls into a course of computational complications renowned for their time-consuming issue known as NP-comprehensive complications. For complications in this class, we do not know any speedier procedures than additional or fewer brute-drive searching by way of each and every achievable alternative. That search room grows exponentially as the size of the trouble raises. For a compact map with only a number of locations, we could manage to exhaustively appear by every feasible 3-coloring right until we uncover a single that performs (or conclude that there is not a single). But the number of strategies to assign three shades to maps with countless numbers of locations is so astronomical that it renders exhaustive search hopeless.
- And four colors? Nicely, that will take about one 2nd or the time you require to say “yes,” simply because every map can be colored with four shades. This is the infamous and lengthy-disputed four-shade theorem.



Francis Guthrie to start with conjectured the 4-colour theorem in 1852 when he found that the counties of England only essential four shades to correctly fill. He suspected this rule would generalize to any map, but while any kindergartner could understand the question, neither he nor his colleagues could demonstrate it. It was crystal clear that a few shades wouldn’t constantly hack it, as evidenced by the diagram under, the place each region neighbors just about every other just one.
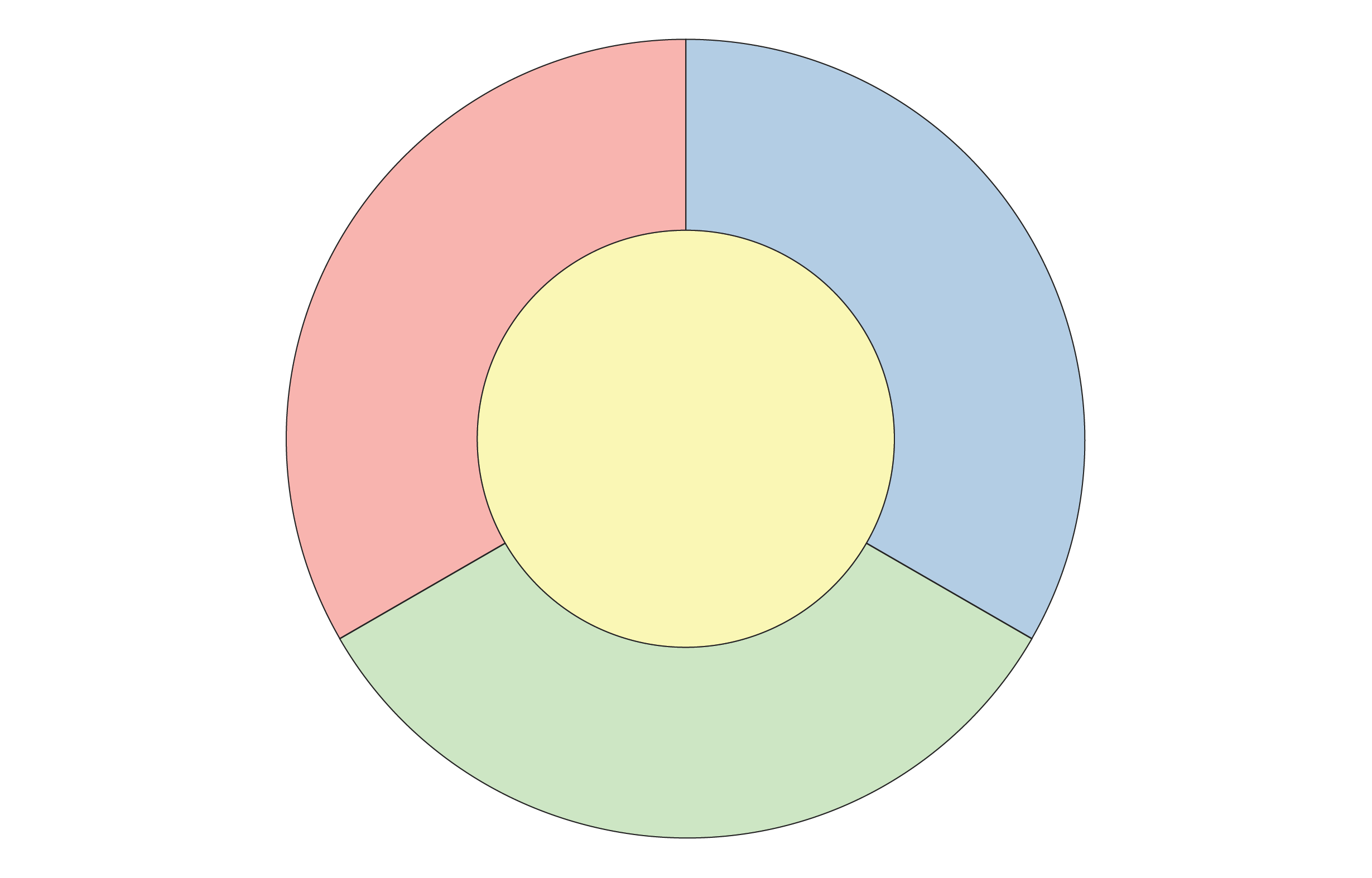


But nobody could obtain a map that required five colors. Stymied by the problem, famed mathematician Augustus De Morgan grew obsessed and concluded that a new axiom—which in math is a statement which is assumed to be accurate without having evidence, from which a lot more challenging statements can be derived—must be added to the foundations of math to take care of Guthrie’s conjecture.
The fevered annoyance ostensibly ended in 1879, when a evidence emerged that 4 hues always suffice. This was underscored by a second independent proof a calendar year afterwards. With the make a difference settled and accolades dispersed, captivated mathematicians returned to their standard research packages. Apart from for some. Eleven many years after the publication of the to start with evidence, both of those proofs were being overturned and the slippery four-colour theorem reverted its position back again to the four-colour conjecture. Percy Heawood, who exposed a gap in the unique evidence, did make some development, while, by proving that 5 colours usually suffice for filling any map. This still left the math world in a instead embarrassing placement. A challenge so seemingly easy had a single of two answers—four or five—but nobody realized which. It would stand this way for almost a century more.
No one could obtain a map necessitating 5 shades, but ruling out the probability of a single completely remained elusive. Because there are an infinite number of maps, 1 could never test just about every of them separately. A critical method toward a answer associated decreasing the dilemma to a finite set of instances that could be checked independently. The leap from infinite to finite appears large, but the monstrous number of instances to check out nevertheless significantly exceeded what any individual could manually process. So mathematicians Kenneth Appel and Wolfgang Haken turned to a daring plan: application a computer to system them instead. In 1976, soon after decades of fantastic-tuning and in excess of a thousand hrs of personal computer time, their algorithm completed exhaustively examining every single situation and the four-color theorem was set up. It was the to start with important theorem to use a computer in its proof.
The math planet lit ablaze with equal sections celebration and dismay. One of Appel and Haken’s colleagues, Bill Tutte, rejoiced that they “Smote the Kraken,” whilst other folks despised the considered of computers encroaching on human ingenuity. The affair also posed a philosophical difficulty in the math local community. Does a proof that just cannot be confirmed by human beings rely as a proof at all? Several anticipated the function to inevitably be retracted, like both of the alleged proofs that preceded it. The New York Times even refused to report on the announcement at initial simply because proofs of the four-shade theorem “have been all wrong anyway.”
A number of makes an attempt to refute the laptop-assisted evidence failed in the adhering to a long time. Mathematicians have due to the fact drastically simplified the proof and confirmed the pc code, but to this day, no proof of the theorem without having the aid of computers is known. The four-colour theorem is now commonly accepted as a point, but nonetheless a yearning lingers about it. A pc system that systematically analyzes reams of configurations does not explain accurately why every single map can be loaded with four hues. While mathematicians now welcome computers as companions in discovery, they even now research nowadays for a more illuminating proof of this colorful puzzle.
This is an viewpoint and analysis posting, and the sights expressed by the writer or authors are not always those people of Scientific American.
[ad_2]
Source hyperlink

