[ad_1]
Creatively tiling a toilet ground is not just a stress filled endeavor for Do it yourself dwelling renovators. It is also one of the hardest difficulties in mathematics. For generations, industry experts have been studying the special homes of tile shapes that can protect floors, kitchen area backsplashes or infinitely large planes with out leaving any gaps. Exclusively, mathematicians are fascinated in tile shapes that can include the whole aircraft with out ever generating a repeating style and design. In these specific circumstances, termed aperiodic tilings, there’s no sample that you can duplicate and paste to hold the tiling heading. No subject how you chop up the mosaic, each and every portion will be exceptional.
Till now, aperiodic tilings usually needed at least two tiles of various shapes. Quite a few mathematicians experienced presently provided up hope of getting a remedy with just one tile, termed the elusive “einstein” tile, which gets its title from the German terms for “one stone.”
Then, past November, retired printing units engineer David Smith of Yorkshire, England, experienced a breakthrough. He found out a 13-sided, craggy form that he considered could be an einstein tile. When he informed Craig Kaplan, a personal computer scientist at the College of Waterloo in Ontario, Kaplan quickly regarded the opportunity of the condition. Together with computer software developer Joseph Samuel Myers and mathematician Chaim Goodman-Strauss of the University of Arkansas, Kaplan proved that Smith’s singular tile does without a doubt pave the plane with no gaps and without repetition. Even improved, they discovered that Smith experienced discovered not only 1 but an infinite amount of einstein tiles. The team just lately claimed its outcomes in a paper that was posted to the preprint server arXiv.org and has not nonetheless been peer-reviewed.
From Attractive Styles to Unprovable Thoughts
Everyone who has walked by way of the breathtaking mosaic corridors of the palace Alhambra in Granada, Spain, is aware the artistry involved in tiling a plane. But these types of elegance harbors unanswerable questions—ones that are, as mathematician Robert Berger stated in 1966, provably unprovable.
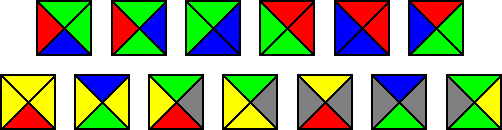 

Suppose you want to tile an infinite floor with an infinite variety of square tiles. You have to stick to a single rule, having said that: the edges of the tiles are colored, and only exact-coloured edges can contact.
With infinite tiles, you commence laying down pieces. You obtain a strategy you think is going to work, but at some stage, you operate into a lifeless conclude. There is a gap you just cannot fill with the tiles you have offered, and you are forced to area mismatched edges next to every other. Video game about.
But undoubtedly, if you experienced the correct tile with the ideal coloration combination, you could have gotten out of your pickle. For instance, possibly you required just 1 tile in which all the edges were being the identical colour. A mathematician would glance at your game and request, “Can you identify irrespective of whether you will strike a dead stop just by hunting at the varieties of colored tiles you were being provided at the commence? This would definitely save you a great deal of time.”
 

The reply, Berger discovered, is no. There will usually be instances where by you simply cannot forecast no matter if you can cover the area without the need of gaps. The offender: the unpredictable, nonrepeating nature of aperiodic tilings. In his function, Berger located an unbelievably huge established of 20,426 differently colored tiles that can pave a aircraft without the need of the color sample at any time repeating itself. And even better, it is bodily unachievable to variety a repeating pattern with that established of tiles, no make any difference how you lay them.
This discovery elevated a further dilemma that has dogged mathematicians ever since: What is the bare minimum range of tile styles that together can build an aperiodic tessellation?
How Very low Can You Go?
In the a long time that followed, mathematicians found lesser and lesser sets of tiles that can develop aperiodic mosaics. Initial, Berger located a single with 104 various tiles. Then, in 1968, laptop scientist Donald Knuth uncovered an case in point with 92. One particular year afterwards mathematician Rafael Robinson uncovered a variant with only six tile types—and at last, in 1974, physicist Roger Penrose presented a answer with only two tiles.
.png) 

Then the development stalled. Several mathematicians have considering the fact that searched for the one-tile answer, the “einstein,” but none had succeeded—including Penrose, who eventually turned his consideration to other puzzles. But David Smith, the 64-yr-previous retiree, hadn’t offered up. He preferred to engage in all over with the PolyForm Puzzle Solver, a piece of software that allows consumers design and assemble tiles, according to the New York Occasions. If a shape looked promising, Smith lower out various paper puzzle parts to experiment with. Then, in November 2022, he arrived throughout the now famed tile that he called the “hat” since of its prime hat shape—though Kaplan emphasizes that a lot of think it seems extra like a T-shirt.
_webp.jpeg) 

When Kaplan gained an e-mail from Smith with the “hat,” it rapidly piqued his curiosity. With the assistance of program, he lined up far more and additional hat-formed tiles, and it seemed as if they could possibly certainly protect the airplane without the need of forming a repeating sample.
But this sort of a repeating sample could nevertheless reveal itself if he retained laying down tiles—perhaps a redundant part would only show up the moment the aircraft was quite a few light-weight-a long time extended. The scientists wanted to mathematically confirm that the tiling was aperiodic. Kaplan turned to Myers and Goodman-Strauss, who experienced worked extensively with tiling in the past.
At 1st, they have been impressed by the simplicity of the opportunity einstein tile because the “hat” has a rather straightforward 13-sided shape. If you had asked Goodman-Strauss what an elusive einstein tile would glimpse like ahead of, “I would’ve drawn some ridiculous, squiggly, terrible matter,” he told Science News. And as the mathematicians took a closer glance at the condition, they recognized that they could participate in with the lengths of the sides and continue to create a seamless, aperiodic mosaic. This a single shape had opened the door to an infinite amount of einstein tiles.
A Never-Repeating Pattern
The mathematicians wanted challenging evidence to back again up their statements. Initially, they utilised approaches that authorities have relied on for a long time to present that specific types of tiles can make aperiodic mosaics. But Myers also went over and above these old methods to build a fully new way to demonstrate it, which may well also be practical for other tilings.
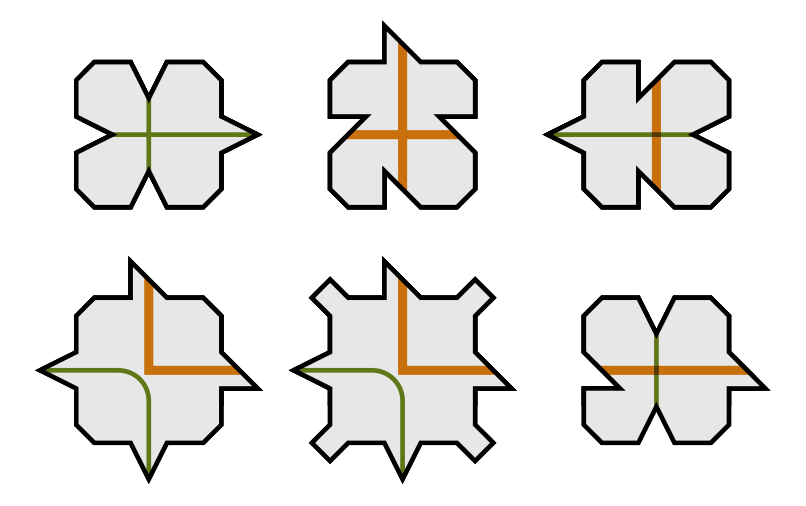 

The tried-and-true system is ideal spelled out applying Robinson’s 6-tile set from 1969. The orange and green traces drawn on Robinson’s tiles operate like the colored edges in the former infinite-squares example. In this article the procedures are equally easy: two Robinson tiles can only be positioned following to every other if the inexperienced and orange lines go on efficiently.
Adhering to this rule results in a recognizable sample consisting of larger and more substantial orange squares. If you continue to keep zooming out, the squares proceed to get larger and intersect with one particular a different. This builds up a hierarchical construction the place just about every part of the mosaic has its exclusive spot. You can’t shift or swap any sections with out breaking the rules and destroying the construction. This tells us that the tessellation will have to be aperiodic.
 

Kaplan, Goodman-Strauss and Myers were being in a position to show something very similar for the hat-formed einstein tile proposed by Smith. To make the tile less complicated to operate with, they smoothed out the hat’s craggy edges into a lot more recognizable and helpful shapes—a single hat tile, for case in point, can be approximated with a triangle. They also utilized clusters of a number of einstein tiles to create unique designs. They could set up 4 hat tiles into a hexagonlike framework, two tiles into a pentagon and an additional mix of two tiles into a parallelogram. These 4 smoothed-out designs, which each individual consisted only of einstein tiles, could then completely address the aircraft in a pattern.
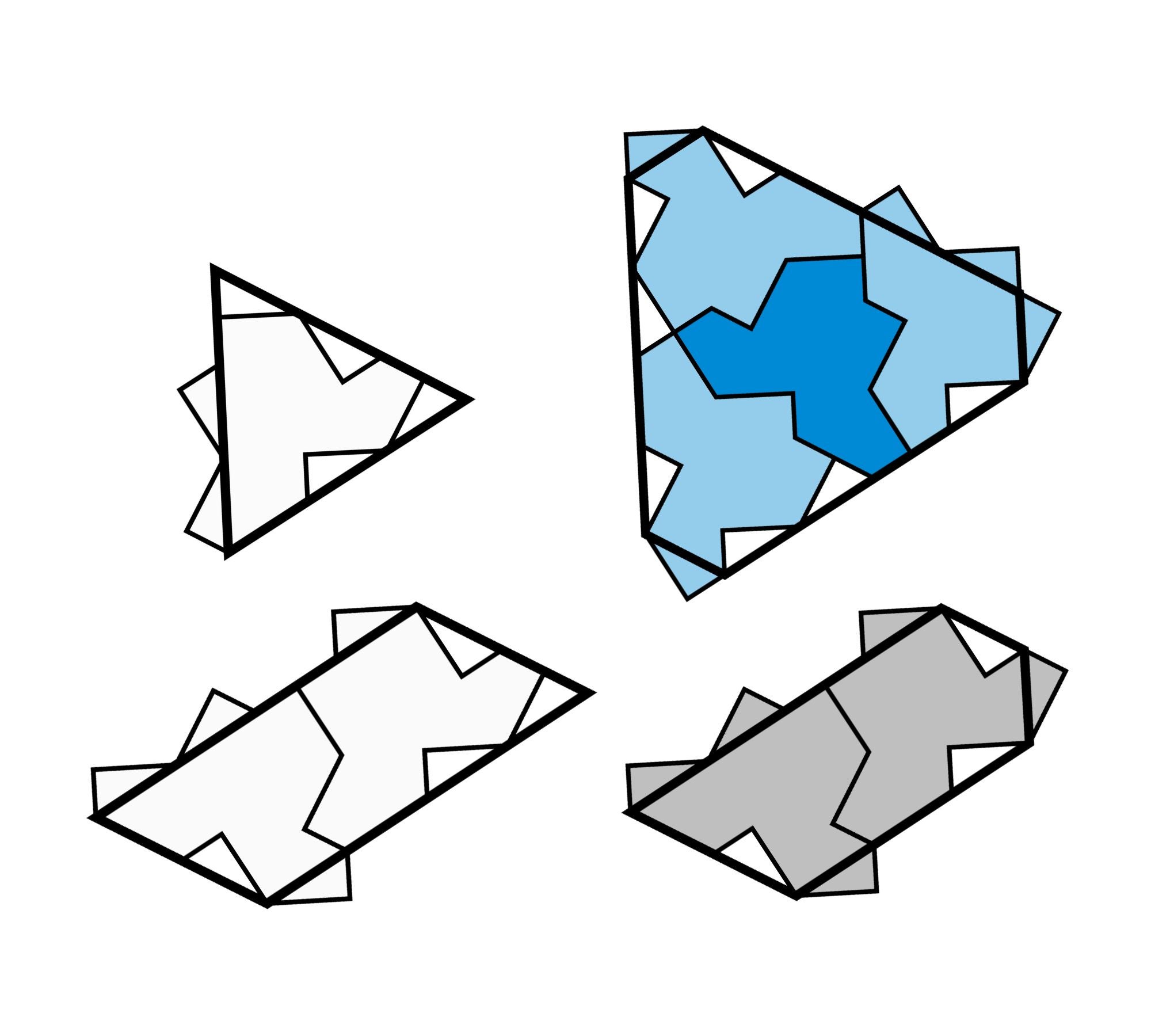 

The mathematicians proved that this tiling contained no repeating patterns because, just like Robinson’s 6-tile set, these 4 particular shapes fashioned hierarchical structures. If you prepare these four einstein tile clusters (hexagon, pentagon, parallelogram and triangle) jointly, they will inevitably generate a more substantial model of just one of all those exact styles. Then, if you mix those people greater designs alongside one another, you will develop even greater variations of those designs, and so on. This process can be recurring indefinitely, giving a hierarchical composition. Therefore, the total sample can’t be split into sections that repeat. If you only slid parts of the pattern to an additional put, that overarching structure would be damaged.
%5B2%5D_webp.jpeg) 

Two Proofs Are Far better Than One particular
This evidence demanded some intricate calculations, so the a few experts enlisted aid from a laptop. They released their computer-assisted proof freely so that anyone could check out it for problems.
But Myers wasn’t contented nonetheless. He developed a new strategy for proving aperiodicity that could be done by hand, without having a personal computer, by demonstrating that the einstein hat is connected to other well-recognized tilings that are a lot easier to analyze. These similar tilings are made of shapes known as polyiamonds, simple tiles formed by combining equilateral triangles. Myers altered some of the einstein hat’s edges to kind two unique polyiamond arrangements that follow the hat’s exact tiling pattern—one shaped like a chevron and the other like a hexagon and a rhombus put jointly. Irrespective of their visible discrepancies, these a few arrangements all have the identical attributes. If the mathematicians could show that both of those of the polyiamond tilings are aperiodic, then the primary tiling must be aperiodic as effectively.
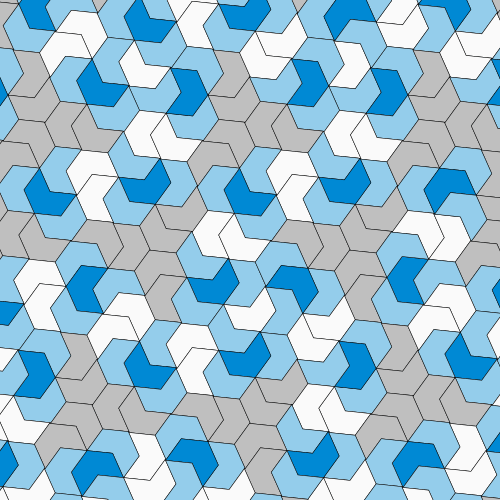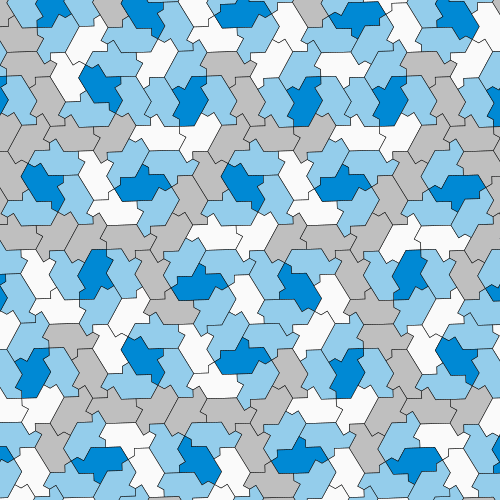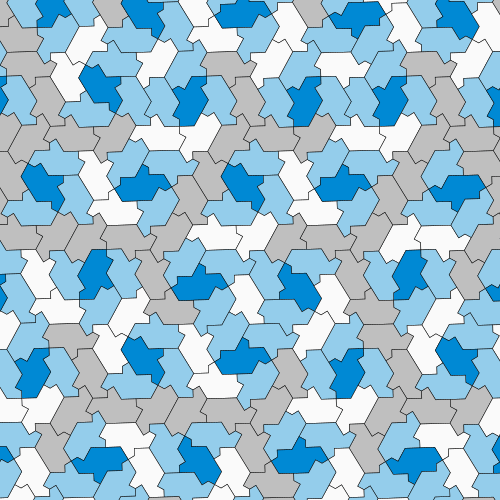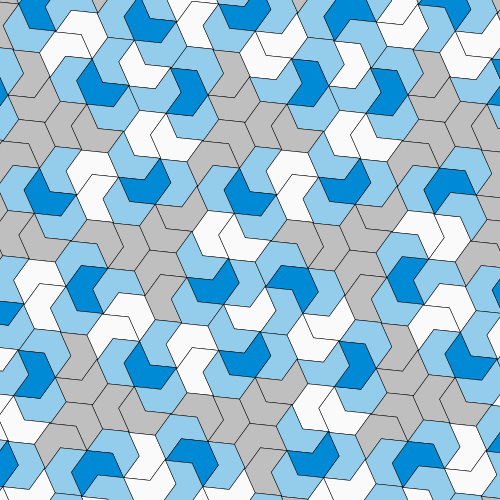 

Luckily, with polyiamonds, that evidence is a matter of primary math. Mathematicians can represent the symmetries of polyiamond arrangements with a amount named a translation vector. If the two new preparations contained repeating patterns, the size of their translation vectors ought to have been relevant to each other—specifically, their ratio really should have been a rational amount. But rather the vectors had a ratio of the sq. root of 2—definitely an irrational number—showing that the polyiamond arrangements weren’t periodic. As a result, the primary hat tile was indeed an einstein.
Myers’s new proof method could also be practical for other tilings, the experts make clear in their paper. But for now, both equally qualified and newbie tilers are just excited to have the long-awaited einstein tile in hand. The home decor prospects are actually infinite. As mathematician Colin Adams of Williams School told New Scientist, “I would put it in my bathroom if I were being tiling it right now.”
This write-up initially appeared in Spektrum der Wissenschaft and was reproduced with authorization.
[ad_2]
Resource hyperlink

